4. Datentypen in C
4.1. Ausdruck
Ein Ausdruck besteht aus einem oder mehreren Operanden, die miteinander durch Operatoren
verknüpft sind. Der Ausdruck hat einen Wert als Ergebnis, der an die Stelle des
Ausdrucks tritt. Der einfachste Ausdruck besteht aus einer einzigen Konstanten oder
Variablen. Die Operatoren müssen zu den Datentypen der Operanden passen.
Beispiele:
25
1 + 2
"Text"
Der Ausdruck a = 1 + 2 ist ein zusammengesetzter Ausdruck. Die
Operanden 1 und 2 sind Zahlenwerte (Literale), die durch den +-Operator
verknüpft werden. Der resultierende Wert 3 tritt nun an die Stelle des Ausdrucks
1 + 2 und wird der Variablen a zugewiesen. Das
Ergebnis des gesamten Ausdrucks ist der Wert von a, also 3.
Daraus folgt, dass in einem Ausdruck mehrere Zuweisungen an Variablen erfolgen
können, z.B. a = b = c = 1 + 2.
Der Wert 3 wird zuerst der Variablen c zugewiesen. Das Ergebnis der
Zuweisung ist der neue Wert von c, also 3. Dieser Wert wird nun der
Variablen b zugewiesen. Das Ergebnis dieser Zuweisung wird
schließlich der Variablen a zugewiesen. Das Ergebnis dieser
Zuweisung wird nicht weiter verarbeitet, da links vom Ausdruck a nichts
mehr steht.
4.2. Ganze Zahlen
Es gibt mehrere verschiedene Repräsentationen von ganzen Zahlen, die sich durch die
Anzahl der verwendeten Bits unterscheiden. Diese heißen short,
int, long und long long.
Letzterer Datentyp wurde erst mit C99 eingeführt. Hierbei gilt: Anzahl Bits von
short <= Anzahl Bits von int <= Anzahl Bits
von long <= Anzahl Bits von long long.
Standard-C schreibt nur die Mindestanzahl der verwendeten Bits vor. Typische Werte für
ein System mit einem 32-Bit-Prozessor sind in der folgenden Tabelle dargestellt. Die
tatsächlichen Werte für Ihr System finden Sie in der Headerdatei
limits.h.
Datentyp |
Mindestanzahl Bits |
Typische Anzahl von Bits |
short |
16 Bits |
16 Bits |
int |
16 Bits |
32 Bits |
long |
32 Bits |
32 Bits |
long long |
64 Bits |
64 Bits |
In der folgenden Tabelle werden die alternativen Schreibweisen für die verschiedenen
Datentypen der ganzen Zahlen aufgeführt:
Datentyp |
alternative Schreibweisen |
||
short |
short int |
signed short |
signed short int |
int |
signed int |
signed |
|
long |
long int |
signed long |
signed long int |
long long |
long long int |
signed long long |
signed long long int |
Das Schlüsselwort signed wurde erst mit C89 eingeführt und
sollte aus Kompatibilitätsgründen mit älteren Compilern weggelassen
werden.
Entsprechend der Anzahl der verwendeten Bits lassen sich unterschiedliche Zahlenbereiche
darstellen:
16 Bits |
-215 |
... |
+215 - 1 |
entspricht |
-32.768 |
... |
+32.767 |
32 Bits |
-231 |
... |
+231 - 1 |
entspricht |
-2.147.483.648 |
... |
+2.147.483.647 |
64 Bits |
-263 |
... |
+263 - 1 |
entspricht |
-9.223.372.036.854.775.808 |
... |
+9.223.372.036.854.775.807 |
Wie oben bereits erwähnt, sind die tatsächlichen Zahlenbereiche für jedes System in der Headerdatei
limits.h als Konstante hinterlegt. Das folgende Beispielprogramm zeigt, wie Sie sich diese
Konstanten anzeigen lassen können.
![]() kap04_01.c
kap04_01.c
01 #include <stdio.h>
02 #include <limits.h>
03
04 int main()
05 {
06 printf("CHAR_BIT = %i\n" , CHAR_BIT ); // Anzahl Bits fuer ein Byte
07 printf("SCHAR_MIN = %i\n" , SCHAR_MIN ); // Min-Wert (signed char)
08 printf("SCHAR_MAX = %i\n" , SCHAR_MAX ); // Max-Wert (signed char)
09 printf("UCHAR_MAX = %i\n" , UCHAR_MAX ); // Max-Wert (unsigned char)
10 printf("CHAR_MIN = %i\n" , CHAR_MIN ); // Min-Wert (char)
11 printf("CHAR_MAX = %i\n" , CHAR_MAX ); // Max-Wert (char)
12 printf("MB_LEN_MAX = %i\n" , MB_LEN_MAX); // max. Anzahl Bytes
13 // fuer ein Multibytezeichen
14 printf("SHRT_MIN = %i\n" , SHRT_MIN ); // Min-Wert (short)
15 printf("SHRT_MAX = %i\n" , SHRT_MAX ); // Max-Wert (short)
16 printf("USHRT_MAX = %i\n" , USHRT_MAX ); // Max-Wert (unsigned short)
17 printf("INT_MIN = %i\n" , INT_MIN ); // Min-Wert (int)
18 printf("INT_MAX = %i\n" , INT_MAX ); // Max-Wert (int)
19 printf("UINT_MAX = %u\n" , UINT_MAX ); // Max-Wert (unsigned int)
20 printf("LONG_MIN = %li\n" , LONG_MIN ); // Min-Wert (long)
21 printf("LONG_MAX = %li\n" , LONG_MAX ); // Max-Wert (long)
22 printf("ULONG_MAX = %lu\n" , ULONG_MAX ); // Max-Wert (unsigned long)
23 printf("LLONG_MIN = %lli\n", LLONG_MIN ); // Min-Wert (long long)
24 printf("LLONG_MAX = %lli\n", LLONG_MAX ); // Max-Wert (long long)
25 printf("ULLONG_MAX = %llu\n", ULLONG_MAX); // Max-Wert (unsigned long long)
26
27 return 0;
28 }
Die Zahlen werden im Rechner als Binärzahlen dargestellt. Dabei werden positive Zahlen
mit führender 0 und negative Zahlen mit führender 1 dargestellt. Um eine positive
Zahl zu negieren, werden alle Bits der Zahl invertiert und anschließend eine 1
addiert. Dieses Verfahren wird Zweier-Komplement-Darstellung (engl:
two-complement notation) genannt. Um beispielsweise die Zahl 2 (8Bit binär:
000000102) zu negieren, werden erst alle Bits invertiert (8Bit binär:
111111012) und anschließend eine 1 addiert. Das Ergebnis lautet dann
-2 (8Bit binär: 111111102).
Zwei Zahlen ändern sich nicht, wenn sie negiert werden: 0 und die kleinste negative
Zahl. Wenn bei der 0 (8Bit binär: 000000002) alle Bits negiert werden
(8Bit binär: 111111112) und anschließend eine 1 addiert wird,
ergibt dies 1000000002. Da es nun aber 9 Bits sind, wird für die Darstellung in
8 Bit das linke Bit "abgeschnitten" und übrig bleibt die 000000002. Wird
die kleinste negative Zahl (8Bit binär: 100000002 = -128 dezimal)
negiert, ergibt sich nach der Negation aller Bits als Zwischenergebnis eine
011111112 und nach der Addition einer 1 die Ausgangszahl
100000002.
Es gibt noch zwei weitere Verfahren, um Zahlen zu negieren, die beide vom Standard-C
akzeptiert werden: Die Einer-Komplement-Darstellung (engl. ones-complement
notation) und die Vorzeichen-Wert-Darstellung (engl. sign magnitude
notation).
In der Einer-Komplement-Darstellung werden - wie bei der Zweier-Komplement-Darstellung -
beim Negieren alle Bits negiert, aber es wird keine 1 mehr addiert. Dadurch reduziert sich
der Zahlenbereich um eins: Mit beispielsweise 16 Bits können dann nur noch die Zahlen
von -32767 bis +32767 dargestellt werden, d.h. die kleinste negative Zahl -32768
entfällt. Dafür gibt es zwei verschiedene Zahlen, die beide den Wert 0 haben:
+0 (binär: 00000000 000000002) und -0
(binär: 11111111 111111112).
In der Vorzeichen-Wert-Darstellung wird beim Negieren nur das Vorzeichen-Bit negiert; die
restlichen Bits bleiben unverändert. Genau wie bei der Einer-Komplement-Darstellung
ist der Zahlenbereich um eins reduziert, da auch hier die kleinste negative Zahl -32768
wegfällt. Für die Zahl 0 gibt es auch hier zwei verschiedene
Darstellungsmöglichkeiten: +0 (binär: 00000000 000000002) und
-0 (binär: 10000000 000000002).
Im weiteren Verlauf werden auf diese beiden alternativen Darstellungsmöglichkeiten
für negative Zahlen nicht weiter eingegangen und statt dessen von der üblichen
Zweier-Komplement-Darstellung ausgegangen.
Durch das Schlüsselwort unsigned wird gekennzeichnet, dass es
sich um rein positive Zahlen handelt. Das Bit, das sonst für das Vorzeichen
benötigt wird, wird hierbei nun für einen größeren Zahlenbereich
verwendet. Die zulässigen Bereiche für ganze positive Zahlen sehen dann wie
folgt aus:
16 Bits |
0 |
... |
+216 - 1 |
entspricht |
0 |
... |
+65.535 |
32 Bits |
0 |
... |
+232 - 1 |
entspricht |
0 |
... |
+4.294.967.295 |
64 Bits |
0 |
... |
+264 - 1 |
entspricht |
0 |
... |
+18.446.744.073.709.551.615 |
Beim Rechnen mit ganzen Zahlen ist die begrenzte Genauigkeit zu beachten, denn die
oben angegebenen Zahlenbereiche sind ja nur eine Untermenge der ganzen Zahlen. Daraus
folgt, dass das Ergebnis einer Folge von arithmetischen Operationen nur dann korrekt
ist, wenn kein Zwischenergebnis den durch den Datentyp vorgegebenen maximalen Zahlenbereich
überschreitet.
![]() kap04_02.c
kap04_02.c
01 #include <stdio.h>
02
03 int main()
04 {
05 short a = 50; /* a,b,c sind short-Zahlen, */
06 short b = 1000; /* also 16 Bit-Zahlen */
07 short c; /* => -32.768 ... 32.767 */
08
09 c = a * b;
10 printf("%i * %i =", a, b);
11 printf("%i\n", c); /* Ergebnis: -15.536 statt 50.000 ! */
12
13 return 0;
14 }
Grundsätzlich immer den größten Datentyp zu verwenden (nach dem Motto:
Sicher ist sicher!), ist nicht sinnvoll, weil Variablen dann mehr Speicherplatz und auch
mehr Rechenzeit benötigen.
Ganze Zahlen können in drei Zahlensystemen verwendet werden:
Oktalzahlen: Wenn eine Zahl mit einer 0 beginnt, wird sie als Oktalzahl interpretiert,
z.B. 0377 = 3778 = 3 * 82 + 7 * 81 + 7 * 80 = 25510 (dezimal).Hexadezimalzahlen: Wenn eine Zahl mit "0x" oder "0X" beginnt, wird sie als Hexadezimalzahl interpretiert,
z.B. 0XAFFE = 45054 dezimal.Dezimalzahlen
4.3. Operatoren für ganze Zahlen
Auf Daten eines bestimmten Typs kann man nur bestimmte Operationen durchführen. Eine
Zeichenkette kann beispielsweise nicht mit einer anderen multipliziert werden. Also:
Ein Operand und der zugehörige Operator gehören zusammen!
Im folgenden werden alle Operatoren für ganze Zahlen aufgelistet:
Arithmetische Operatoren:
Operator |
Beispiel |
Bedeutung |
+ |
+i |
unäres Plus (kann weggelassen werden) |
- |
-i |
unäres Minus |
++ |
++i |
vorherige Inkrementierung (Erhöhung um 1) |
|
i++ |
nachfolgende Inkrementierung |
-- |
--i |
vorherige Dekrementierung (Erniedrigung um 1) |
|
i-- |
nachfolgende Dekrementierung |
+ |
i + 2 |
binäres Plus (Addition) |
- |
i - 5 |
binäres Minus (Subtraktion) |
* |
5 * i |
Multiplikation |
/ |
i / 6 |
Division |
% |
i % 4 |
Modulo (Divisionsrest) |
= |
i = 3 + j |
Zuweisung |
Arithmetische Kurzform-Operatoren:
Operator |
Beispiel |
Bedeutung |
+= |
i += 3 |
i = i + 3 |
-= |
i -= 3 |
i = i - 3 |
*= |
i *= 3 |
i = i * 3 |
/= |
i /= 3 |
i = i / 3 |
%= |
i %= 3 |
i = i % 3 |
Relationale Operatoren:
Operator |
Beispiel |
Bedeutung |
< |
i < 3 |
kleiner als |
> |
i > 3 |
größer als |
<= |
i <= 3 |
kleiner als oder gleich |
>= |
i >= 3 |
größer als oder gleich |
== |
i == 3 |
gleich |
!= |
i != 3 |
ungleich |
4.4. Bitoperatoren
Weil ganze Zahlen auch als Bitvektoren aufgefasst werden können, sind
zusätzlich Bitoperationen möglich. Dabei werden die Zahlen in
Binärdarstellung betrachtet.
Beispiele:
int a = 5, b;
b = a << 2;
Dies bewirkt eine Bitverschiebung um 2 Stellen nach links, wobei von rechts Nullen nachgezogen
werden (beim Verschieben nach rechts werden von links Nullen nachgezogen; bei vorzeichenbehafteten
Zahlen wird - je nach Compiler - entweder eine Null oder das Vorzeichen nachgezogen). Dies
entspricht der Multiplikation mit 22, also mit 4.
0000 0000 0000 0101 binäre Darstellung der Zahl 5
0000 0000 0001 0100 alle Bits um 2 Stellen nach links verschoben
Die Variable a hat nun den Wert 20 (0000 0000 0001 01002).
a = a & b;
Diese Anweisung bewirkt eine bitweise UND-Verknüpfung, d.h. das Ergebnis-Bit ist 1,
wenn die Bits der beiden Operanden auch gleich 1 sind, ansonsten 0. In der binären
Darstellung sind das wie folgt aus:
0000 0000 0001 0100 binäre Darstellung der Zahl 20
0000 0000 0000 0101 binäre Darstellung der Zahl 5
0000 0000 0000 0100 bitweises UND; Ergebnis: 4
In den folgenden zwei Tabellen werden alle Bit-Operatoren aufgelistet.
Bitoperatoren:
Operator |
Beispiel |
Bedeutung |
<< |
i << 2 |
Bits nach links schieben (Multiplikation mit 2er-Potenzen) |
>> |
i >> 1 |
Bits nach rechts schieben (Division durch 2er-Potenzen) |
& |
i & 7 |
bitweises UND |
^ |
i ^ 7 |
bitweises Exklusiv-ODER (XOR) |
| |
i | 7 |
bitweises ODER |
~ |
~i |
bitweises Negieren |
Bit-Kurzform-Operatoren:
Operator |
Beispiel |
Bedeutung |
<<= |
i <<= 2 |
i = i << 2 |
>>= |
i >>= 1 |
i = i >> 1 |
&= |
i &= 3 |
i = i & 3 |
^= |
i ^= 3 |
i = i ^ 3 |
|= |
i |= 3 |
i = i | 3 |
4.5. Reelle Zahlen
Reelle Zahlen, auch Fließkomma- oder Gleitkommazahlen genannt, bauen sich
folgendermaßen auf:
- Vorzeichen (optional)
- Vorkommastellen
- Dezimalpunkt (KEIN Komma!)
- Nachkommastellen
- e oder E und Ganzzahl-Exponent (optional)
- Suffix f,F oder l,L (optional)
(f,F für
float; l, L für
long double; Zahlen ohne Suffix sind vom Typ double)
Einige Beispiele für reelle Zahlen sind:
-236.265e6f
3.4E3
3.1415
1e-08
9.2L
Mit dem Exponenten sind Zehnerpotenzen gemeint, d.h. 3.4E3 ist also identisch mit
3.4 * 103 oder 3400.
Reelle Zahlen werden durch drei Datentypen dargestellt. Sie sind ähnlich wie bei den
ganzen Zahlen durch Zahlenbereiche eingeschränkt, bedingt durch die Anzahl der
verwendeten Bits pro Zahl. Die angegebenen Bits sowie die Genauigkeiten sind beispielhaft,
da sie von System zu System variieren.
| Typ | Bits | Zahlenbereich | Stellen Genauigkeit |
| float | 32 | +/-1.17549 * 10-38 ... +/-3.40282 * 1038 | 7 |
| double | 64 | +/-2.22507 * 10-308 ... +/-1.79769 * 10308 | 15 |
| long double | 80 | +/-3.3621 * 10-4932 ... +/-1.18973 * 104932 | 19 |
Genauso wie bei den ganzen Zahlen gibt es auch für die Fließkommazahlen eine Headerdatei, in der die
Zahlenbereiche für das aktuelle System als Konstante hinterlegt sind. Diese Headerdatei heißt
float.h. Im folgenden Beispielprogramm wird gezeigt, wie Sie sich diese Konstanten
anzeigen lassen können.
![]() kap04_03.c
kap04_03.c
01 #include <stdio.h>
01 #include <float.h>
03
04 int main()
05 {
06 // FLT: float; DBL: double; LDBL: long double
07 printf("FLT_RADIX = %i\n" , FLT_RADIX ); // Basis Exponentendarst.
08 printf("FLT_MANT_DIG = %i\n" , FLT_MANT_DIG ); // Anz. Stellen Mantisse
09 printf("DBL_MANT_DIG = %i\n" , DBL_MANT_DIG );
10 printf("LDBL_MANT_DIG = %i\n" , LDBL_MANT_DIG );
11 printf("FLT_DIG = %i\n" , FLT_DIG ); // Genauigkeit Dez.ziffern
12 printf("DBL_DIG = %i\n" , DBL_DIG );
13 printf("LDBL_DIG = %i\n" , LDBL_DIG );
14 printf("FLT_MIN_EXP = %i\n" , FLT_MIN_EXP ); // min. neg. FLT_RADIX-Exp.
15 printf("DBL_MIN_EXP = %i\n" , DBL_MIN_EXP );
16 printf("LDBL_MIN_EXP = %i\n" , LDBL_MIN_EXP );
17 printf("FLT_MIN_10_EXP = %i\n" , FLT_MIN_10_EXP ); // min. neg. 10er-Exponent
18 printf("DBL_MIN_10_EXP = %i\n" , DBL_MIN_10_EXP );
19 printf("LDBL_MIN_10_EXP = %i\n" , LDBL_MIN_10_EXP);
20 printf("FLT_MAX_EXP = %i\n" , FLT_MAX_EXP ); // max. FLT_RADIX-Exponent
21 printf("DBL_MAX_EXP = %i\n" , DBL_MAX_EXP );
22 printf("LDBL_MAX_EXP = %i\n" , LDBL_MAX_EXP );
23 printf("FLT_MAX_10_EXP = %i\n" , FLT_MAX_10_EXP ); // max. 10er-Exponent
24 printf("DBL_MAX_10_EXP = %i\n" , DBL_MAX_10_EXP );
25 printf("LDBL_MAX_10_EXP = %i\n" , LDBL_MAX_10_EXP);
26 printf("FLT_MAX = %g\n" , FLT_MAX ); // max. Fließkommawert
27 printf("DBL_MAX = %g\n" , DBL_MAX );
28 printf("LDBL_MAX = %Lg\n", LDBL_MAX );
29 printf("FLT_EPSILON = %g\n" , FLT_EPSILON ); // kleinster Wert, fuer den
30 printf("DBL_EPSILON = %g\n" , DBL_EPSILON ); // 1.0 + x ungleich 1.0
31 printf("LDBL_EPSILON = %Lg\n", LDBL_EPSILON ); // gilt
32 printf("FLT_MIN = %g\n" , FLT_MIN ); // min. Fließkommawert
33 printf("DBL_MIN = %g\n" , DBL_MIN );
34 printf("LDBL_MIN = %Lg\n", LDBL_MIN );
35
36 return 0;
37 }
Eine beliebige Genauigkeit ist allerdings nicht für alle Zahlen möglich! Für
die Darstellung der reellen Zahlen mit 32 Bits beispielsweise existieren nur 232
= 4.294.967.296 verschiedene Möglichkeiten, eine Zahl zu bilden. Ein reelles
Zahlenkontinuum ist das nun nicht gerade und alle Illusionen von der computertypischen
Genauigkeit und Korrektheit sind über den Haufen geschmissen! Mögliche Folgen der
nicht exakten Darstellung können sein:
Werden zwei fast gleich große Werte subtrahiert, heben sich die signifikanten Ziffern auf und das Ergebnis ist ungenau (numerische Auslöschung).
Die Division durch betragsmäßig zu kleine Werte hat einen Überlauf (Overflow) zum Ergebnis, d.h. das Ergebnis liegt außerhalb des Zahlenbereiches des Datentyps. Ähnlich ist es bei der Unterschreitung (Underflow). Diese tritt auf, wenn das Ergebnis zu klein ist, als das es mit dem gegebenen Datentyp dargestellt werden kann. Das Ergebnis wird dann auf 0 gesetzt.
Die Reihenfolge einer Berechnung kann entscheidend sein! Wenn beispielsweise die drei Variablen a, b und c addiert werden sollen, ist es mathematisch gesehen kein Unterschied, ob zuerst a und b addiert und zu diesem Ergebnis c addiert wird oder ob zuerst b und c addiert und dann a dazuaddiert wird. Anders dagegen beim Computer und der Programmiersprache C/C++. Andere Programmiersprachen haben die gleichen oder ähnliche Probleme. Daher muss zu kritischen Berechnungen auch immer eine Genauigkeitsbetrachtung gemacht werden!
Beispiel für Probleme mit der Rechengenauigkeit:
![]() kap04_04.c
kap04_04.c
01 #include <stdio.h>
02
03 int main()
04 {
05 float a = 1.234567E-9f, b = 1.000000f, c = -b;
06 float s1, s2;
07
08 s1 = a + b;
09 s1 += c;
10 s2 = b + c;
11 s2 += a;
12 printf("%e\n", s1); /* Erg.: 0.000000e+00 */
13 printf("%e\n", s2); /* Erg.: 1.234567e-09 */
14
15 return 0;
16 }
Der interne Aufbau einer Fließkommazahl ist durch den IEEE Standard for Binary
Floating-Point Arithmetic (ISO/IEEE Standard 754-1985) oder kurz IEEE Standard 754
festgelegt. Dieser wird im folgenden anhand des Datentyps float
vorgestellt:
Bei einer 32Bit-float-Zahl ist das ganz linke Bit für das
Vorzeichen S, die nächsten 8 Bits von links (Bit 2 bis 9) bilden den
vorzeichenlosen Exponenten E und die restlichen 23 Bits die Mantisse M
(nicht vergleichbar mit einer Mantisse im mathematischen Sinne). Die Zahl f wird
dann wie folgt berechnet:
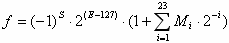
, wobei Mi das i-te Bit der Mantisse von links ist.
Beispiel:
float-Zahl binär dargestellt: 00111101 11001100 11001100 110011012
Dann ist S gleich 0, E gleich 011110112 (gleich 123 dezimal) und M gleich
100110011001100110011012. Diese Werte werden in die Formel eingesetzt:
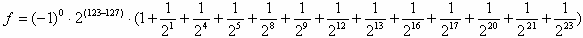
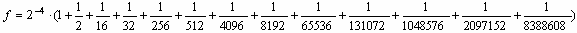
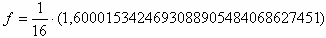
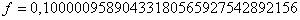
Bei sieben Stellen Genauigkeit (1 Stelle vor und 6 Stellen nach dem Komma) ergibt diese
Zahl also 0,1.
Es sind nun noch einige Sonderfälle zu betrachten:
Exponent E gleich 255: |
||
|
Mantisse M ungleich 0: |
f = NaN (Not a Number) |
|
Mantisse M gleich 0: |
f = +/- Infinity (Unendlich; entsprechend des Vorzeichens S) |
Exponent E gleich 0: |
||
|
Mantisse M ungleich 0: |
Zahl ist nicht normalisiert und lässt sich wie folgt berechnen: |
|
Mantisse M gleich 0: |
f = +/- 0 (entsprechend des Vorzeichens S) |
4.6. Operatoren für reelle Zahlen
Die Operatoren für reelle Zahlen sind die folgenden:
Arithmetische Operatoren:
Operator |
Beispiel |
Bedeutung |
+ |
+f |
unäres Plus (kann weggelassen werden) |
- |
-f |
unäres Minus |
+ |
f + 2 |
binäres Plus (Addition) |
- |
f - 5 |
binäres Minus (Subtraktion) |
* |
5 * f |
Multiplikation |
/ |
f / 6 |
Division |
= |
f = 3 + g |
Zuweisung |
Arithmetische Kurzform-Operatoren:
Operator |
Beispiel |
Bedeutung |
+= |
f += 3 |
f = f + 3 |
-= |
f -= 3 |
f = f - 3 |
*= |
f *= 3 |
f = f * 3 |
/= |
f /= 3 |
f = f / 3 |
Relationale Operatoren:
Operator |
Beispiel |
Bedeutung |
< |
f < 3 |
kleiner als |
> |
f > 3 |
größer als |
<= |
f <= 3 |
kleiner als oder gleich |
>= |
f >= 3 |
größer als oder gleich |
== |
f == 3 |
gleich |
!= |
f != 3 |
ungleich |
4.7. Regeln zum Bilden von Ausdrücken
Es gelten im allgemeinen die Regeln der Algebra beim Berechnen eines Ausdrucks, z.B.
Klammerregeln und Punkt- vor Strichrechnung. In der folgenden Tabelle werden die
Prioritäten der einzelnen Operatoren aufgelistet. Dabei ist die Priorität 1 die
höchste und 16 die niedrigste Priorität.
| Priorität | Operator | Reihenfolge |
1 |
[] |
links nach rechts |
2 |
++ -- (prefix) |
rechts nach links |
3 |
(type name) (Typkonvertierung) |
rechts nach links |
4 |
* / % |
links nach rechts |
5 |
+ - |
links nach rechts |
6 |
<< >> |
links nach rechts |
7 |
< > <= >= |
links nach rechts |
8 |
== != |
links nach rechts |
9 |
& (bitweises UND) |
links nach rechts |
10 |
^ (bitweises Exklusiv-ODER) |
links nach rechts |
11 |
| (bitweises ODER) |
links nach rechts |
12 |
&& (logisches UND) |
links nach rechts |
13 |
|| (logisches ODER) |
links nach rechts |
14 |
?: |
rechts nach links |
15 |
alle Zuweisungen wie |
rechts nach links |
16 |
, |
links nach rechts |
Auf gleicher Prioritätsstufe wird ein Ausdruck von links nach rechts abgearbeitet.
Dies wird auch linksassoziativ genannt. Ausnahme: Die unären und
Zuweisungsoperatoren werden von rechts nach links abgearbeitet (rechtsassoziativ).
Generell werden aber zuerst immer die Klammern ausgewertet.
Beispiele:
a = b + c + d; ist gleich mit
a = ((b + c) + d);
a = b = c = d; ist gleich mit
a = (b = (c = d));
Die Auswertungsreihenfolge der Teilausdrücke einer Priorität untereinander ist
jedoch nicht festgelegt und kann von jedem Compiler anders gesetzt werden. Daher sollte es
vermieden werden, in einem Ausdruck einen Wert gleichzeitig zu verändern und zu
benutzen, wie es die folgenden Beispiele zeigen:
Beispiele:
int Teil = 0;
Summe = (Teil = 3) + (++Teil);
Das Ergebnis von Summe kann sowohl den Wert 4 als auch den Wert 7
annehmen, je nachdem welche Klammer zuerst ausgewertet wird.
int i = 2;
i = 3 * i++;
Erste Möglichkeit: Es wird 3 * i berechnet und das Ergebnis 6 wird
der Variablen i zugewiesen. Anschließend wird
i um 1 erhöht. Das Endergebnis ist dann 7.
Zweite Möglichkeit: Es wird 3 * i berechnet. Nun wird
i um 1 (von 2 auf 3) erhöht. Anschließend wird aber
i das Ergebnis der Berechnung 3 * i zugewiesen.
Das Endergebnis ist in diesem Fall 6.
4.8. Zeichen
Zeichen sind Buchstaben wie a, B,
C, d, Ziffernzeichen wie 4,
5, 6 und Sonderzeichen wie ;,.!
sowie andere Zeichen. Für sie gibt es den Datentyp char. Der
Datentyp Zeichen beinhaltet immer nur ein Zeichen, das durch eine 1-Byte-Zahl (ganze Zahl)
intern gespeichert wird. Daraus folgt, dass es 256 verschiedene Zeichen geben kann.
Davon sind die ersten 128 international festgelegt, während die anderen 128 regional
unterschiedlich sind (diese werden für nationale Sonderzeichen genutzt). Der
Zusammenhang zwischen den Zeichen und den intern gespeicherten Zahlen ist in der
sogenannten
ASCII-Tabelle
festgelegt (siehe Kapitel 14 im Skript "Grundlagen der Informatik").
Konstante Zeichen werden in Hochkommata eingeschlossen, also beispielsweise
'y', '9', '?'.
Hinweis: Speziell bei den Ziffernzeichen muss zwischen dem
Zeichen (z.B. '1') und der Ziffer (z.B. 1)
unterschieden werden!
Es wird generell zwischen den Datentypen signed char (interner
Zahlenbereich: -128 ... +127) und unsigned char (interner
Zahlenbereich: 0 ... 255) unterschieden. Meist wird aber nur char
verwendet, wobei damit bei den meisten Compilern der Datentyp
signed char gemeint ist.
Da Zeichen intern als ganze Zahlen gespeichert werden, können alle Operatoren der
ganzen Zahlen auch auf Zeichen angewendet werden, wobei nicht alle Operationen auch Sinn
machen (beispielsweise die Addition zweier Zeichen). Daher noch einmal eine Tabelle mit den
Operatoren, die für Zeichen sinnvoll sind (a ist eine Variable vom Typ
char).
Operator |
Beispiel |
Bedeutung |
= |
a = 'X' |
Zuweisung |
< |
a < 'z' |
kleiner als |
> |
a > 'c' |
größer als |
<= |
a <= 'M' |
kleiner als oder gleich |
>= |
a >= 'k' |
größer als oder gleich |
== |
a == 'J' |
gleich |
!= |
a != 'n' |
ungleich |
Es gibt besondere Zeichenkonstanten, die nicht direkt gedruckt bzw. auf dem Bildschirm
angezeigt werden können. Um diese darzustellen, werden sie als zwei Zeichen
geschrieben, benötigen aber wie alle Zeichen nur ein Byte. Das erste der zwei Zeichen
ist ein Backslash ('\'). Diese Zeichen werden auch
Escape-Sequenzen genannt, weil der Backslash als Escape-Zeichen
verwendet wird, um der normalen Interpretation als ein einzelnes Zeichen zu entkommen (to
escape). In der nächsten Tabelle werden einige dieser Escape-Sequenzen aufgelistet.
Zeichen |
Bedeutung |
\a |
Signalton |
\f |
Seitenvorschub |
\n |
neue Zeile |
\r |
Zeilen- oder Wagenrücklauf |
\t |
Tabulator |
\\ |
Backslash \ |
\' |
Hochkomma ' |
\" |
Anführungszeichen " |
\0 |
Nullbyte (z.B. für String-Ende) |
\? |
Fragezeichen ? (C99) |
4.9. Multibyte und Wide Characters
Ein Wide Character wird durch den Datentyp wchar_t dargestellt und ist
auf den meisten Systemen als int definiert (in der Headerdatei
stddef.h). Ein Array von Wide Characters ist ein Wide String.
4.10. Logischer Datentyp
Vor dem C99-Standard gab es keinen direkten logischen Datentypen. Statt dessen werden die
logischen Werte durch ganze Zahlen dargestellt. Dabei wird eine ganze Zahl ungleich Null
als logischen Wert wahr (im englischen: true) und eine ganze Zahl gleich Null als
falsch (im englischen: false) interpretiert. Ergebnisse von logischen Operationen sind
gleich 1 für wahr und gleich 0 für falsch.
Beispiel:
int i = 17, j;
j = !i; /* ergibt 0 (falsch), da i ungleich 0 (wahr) ist */
i = !j; /* ergibt 1 (wahr), da j gleich 0 (falsch) ist */
Erst mit C99 wurde ein logischer Datentyp eingeführt: _Bool. Aber
auch dieser Datentyp ist eine ganze Zahl, der allerdings nur die Zahlen 0 und 1 (für
falsch und wahr) speichern kann.
Zusätzlich wurde mit dem C99-Standard die Headerdatei stdbool.h
eingeführt. In ihr werden das Makro bool als Datentyp sowie die
Konstanten false und true (0 und 1) definiert.
Dies sind Definitionen und keine Schlüsselwörter (im Gegensatz zum Datentyp
_Bool)! Dies ist gerade für ältere C-Programme wichtig, da
in diesen meistens der Datentyp bool mit den Konstanten
false und true vom Programmierer selber definiert
wurde. In diesen Fällen sollte diese Headerdatei nicht eingefügt werden.
Da logische Variablen intern als ganze Zahlen gespeichert werden, können alle
Operatoren der ganzen Zahlen hier auch angewendet werden, wobei nicht alle Operationen auch
Sinn machen (beispielsweise die Addition wahr und wahr). Daher noch einmal eine Tabelle mit
den Operatoren, die für logische Variablen sinnvoll sind.
Operator |
Beispiel |
Bedeutung |
! |
!i |
logische Negation |
&& |
i && j |
logisches UND |
|| |
i || j |
logisches ODER |
= |
h = i && j |
Zuweisung |
Werden mehrere Bedingungen mit einem logischen Und oder einem logischen Oder verknüpft, ist zu beachten,
dass die Compiler im allgemeinen versuchen, die Ermittlung des Ergebnisses der verknüpften Bedingungen zu
optimieren. Das bedeutet, dass bei einem logischen Und die zweite Bedingung nur dann ausgewertet wird, wenn die
erste Bedingung wahr ist. Denn ist die erste Bedingung falsch, ist beim logischen Und auch das Ergebnis der
Verknüpfung falsch, ganz gleich wie die zweite Bedingung aussieht. Und bei einem logischen Oder wird die
zweite Bedingung nur dann ausgewertet, wenn die erste Bedingung falsch ist. Denn ist die erste Bedingung wahr,
ist beim logischen Oder auch das Ergebnis der Verknüpfung unabhängig von der zweiten Bedingung wahr.
Dabei können unangenehme Seiteneffekte entstehen!
Im folgenden Beispiel wird diese Optimierung ausgenutzt:
![]() kap04_05.c
kap04_05.c
01 #include <stdio.h>
02
03 int main()
04 {
05 int a = 0, b = 1;
06 char Zeichen = 'A';
07
08 (a && (Zeichen = 'B'));
09 printf("Zeichen = %c\n", Zeichen);
10
11 (b || (Zeichen = 'C'));
12 printf("Zeichen = %c\n", Zeichen);
13
14 return 0;
15 }
Durch die Optimierung werden die beiden Zuweisungen der Zeichen 'B' und
'C' nicht ausgeführt und es wird
Zeichen = A
Zeichen = A
ausgegeben. Diese Optimierung ist aber nicht vorgeschrieben. Und ohne Optimierung würden die beiden
Zuweisungen ausgeführt werden und das Ergebnis sieht anders aus. Von daher sollte das Programm wie
folgt umgeschrieben werden, um in jedem Fall das obige Ergebnis zu erhalten.
![]() kap04_06.c
kap04_06.c
01 #include <stdio.h>
02
03 int main()
04 {
05 int a = 0, b = 1;
06 char Zeichen = 'A';
07
08 if (a)
09 Zeichen = 'B';
10 printf("Zeichen = %c\n", Zeichen);
11
12 if (!b)
13 Zeichen = 'C';
14 printf("Zeichen = %c\n", Zeichen);
15
16 return 0;
17 }
4.11. Konvertierung zwischen den Datentypen (Typumwandlung)
Da die Zeichen und der logische Datentyp intern als ganze Zahlen gespeichert werden, liegt
es nahe, zwischen den Datentypen konvertieren zu wollen. Dabei muss aber
berücksichtigt werden, dass sich nicht jeder Datentyp zu 100% konvertieren
lässt; beispielsweise wenn eine reelle Zahl in eine ganze Zahl konvertiert wird,
gehen alle Nachkommastellen verloren. Durch die Konvertierung wird die Typkontrolle des
Compilers umgangen und kann daher sehr schnell zu Fehlern führen.
Zum Konvertieren gibt es mehrere Möglichkeiten. Hier wird nur die erste Variante
vorgestellt (die anderen werden im C++-Teil beschrieben). Dazu wird zuerst der Datentyp, in
den konvertiert werden soll, und dahinter der Wert bzw. die Variable geschrieben. Dabei
wird der Datentyp in Klammern gesetzt. Diese Konvertierung wird auch
explizite Konvertierung bzw. explizite Typumwandlung genannt.
Beispiel:
char c = 'A';
int i;
i = (int) c;
Der ASCII-Wert des Buchstaben A (65) wird als ganze Zahl der Variablen i zugeordnet. Auch umgekehrt
- bei der Konvertierung von ganzen Zahlen nach Zeichen - wird die
ASCII-Tabelle verwendet.
Beispiel:
char c;
int i = 97;
c = (char) i; /* ergibt ein 'a' */
Um von Ziffernzeichen ('0', '1', ...) nach Ziffern zu konvertieren, wird das Ziffernzeichen in eine ganze Zahl konvertiert
und dann der ASCII-Wert des Ziffernzeichens '0' abgezogen.
Beispiel:
int i;
i = (int) '5' - (int) '0';
Bei diesem Beispiel ist der Wert der Variablen i gleich 5 (ASCII-Wert von '5' ist 53 und der ASCII-Wert von '0' ist 48).
Auch für die Umwandlung von Klein- in Großbuchstaben oder umgekehrt können die ASCII-Werte der Zeichen
verwendet werden. Um von Klein- nach Großbuchstaben zu kommen, muss das Zeichen in eine Zahl umgewandelt werden,
von dieser Zahl der Wert 32 abgezogen (von Groß- nach Kleinbuchstaben: dazuaddiert) und anschließend wieder in
ein Zeichen umgewandelt werden.
Beispiel:
char c = 'A';
c = (char) ((int) c + 32); /* Umwandlung in Kleinbuchstaben */
/* oder kurz: */
c = c + 32;
/* oder noch kürzer: */
c += 32;
Die kurzen Fassungen sind implizite Konvertierungen bzw. implizite Typumwandlungen.
Dabei wird der Datentyp, in den konvertiert werden soll, weggelassen. Dies kann nur zwischen Zeichen
und ganzen Zahlen sowie zwischen logischen Datentypen und ganzen Zahlen angewendet werden. Aber auch
zwischen den ganzen Zahlen (z.B. short nach long oder
long nach int) sowie zwischen den reellen Zahlen
(z.B. double nach float) können implizite
Konvertierungen verwendet werden (unter Berücksichtigung der Zahlenbereiche und mit
evtl. Genauigkeitsverlust).
Hinweis: Bei der Konvertierung einer ganzen Zahl größer als 255 in ein
Zeichen werden die überzähligen Bits nicht berücksichtigt.
Voriges Kapitel: 3. Variablen
Nächstes Kapitel: 5. Einfache Ein- und Ausgabe in C